문제
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다.
크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다.
***
* *
***N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다. 예를 들어 크기 27의 패턴은 예제 출력 1과 같다.
풀이
완전탐색 알고리즘에서 분할정복 알고리즘을 이용해서 푸는 문제다.
재귀를 이용해서 풀면쉽게 풀 수 있다.
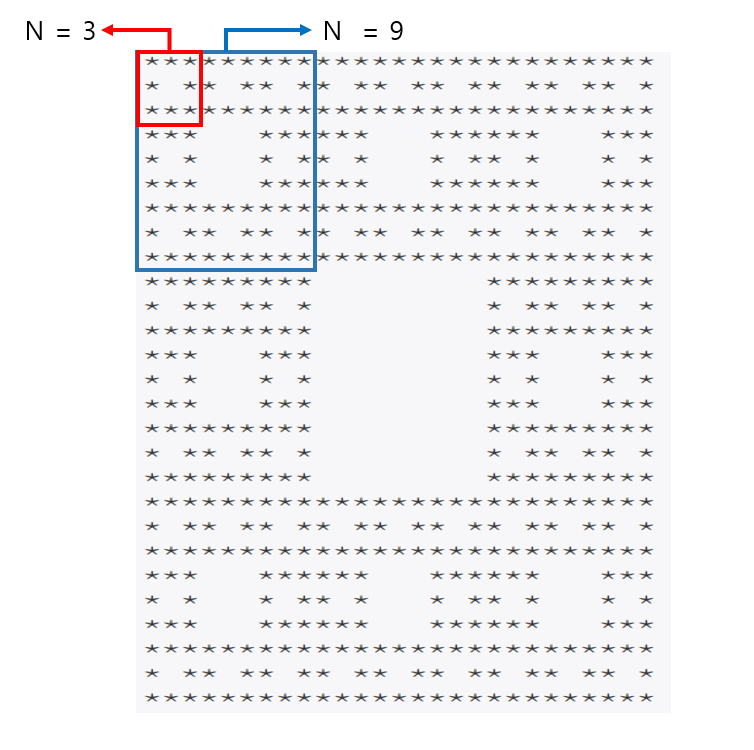
N = 27 일 때, 그림을 보면 N = 9 인 도형이 총 8개 있는 것을 알 수 있다.
N = 9 일 때, 그림을 보면 N = 3 인 도형이 총 8개 있는 것을 알 수 있다.
N = 3 일 때, 그림을 보면 N = 1 인 도형이 총 8개 있는 것을 알 수 있다.
재귀적으로 풀 수 있는 감이 온다.
제일 윗줄에 n / 3 의 도형이 총 3개
두번째 줄에 n / 3 의 도형이 총 2개 빈공간이 (n / 3) * (n /3) 크기만큼 존재한다.
세번째 줄에 n / 3 의 도형이 총 3개
이 규칙을 이용하여 재귀적으로 코드를 짜면
static void printStar(int n, int x, int y) {
if( n == 1) {
cube[y][x] = "*";
return;
}
for(int j = 0 ; j < 3 ; j++) {
//첫번째 줄과 세번째 줄엔 n/3 의 모양이 총 3개
if( j != 1) {
for(int i = 0 ; i < 3 ; i++) {
printStar(n / 3, y + j * n / 3, x + i * n / 3);
}
}
//두번째 줄엔 n/3의 모양이 양쪽 끝에 두개 가운데는 빈공간
else {
for(int i = 0 ; i < 3 ; i++) {
if(i != 1) {
printStar(n / 3, y + j * n / 3, x + i * n / 3);
}
else {
printSpace(n / 3, y + j * n / 3, x + i * n / 3);
}
}
}
}
}위와 같은 코드가 나온다.
printStar()를 이용해서 별을 찍는다. n = 1 이 됐을때 해당 위치에 별을 찍어주면 된다.
printSpace()를 이용해서 (3 / n) * (3 / n) 크기의 빈공간을 찍어준다.
이렇게 코드를 짜고 이차배열을 선언하여 저장하고 출력하면 된다.
<전체코드>
import java.io.*;
import java.util.*;
public class Main {
static StringBuilder sb = new StringBuilder();
static String[][] cube;
public static void main(String[] args) throws IOException{
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(bufferedReader.readLine());
cube = new String[n + 1][n + 1];
printStar(n, 1, 1);
for(int i = 1 ; i <= n ; i++) {
for(int j = 1 ; j <= n ; j++) {
sb.append(cube[i][j]);
}
sb.append("\n");
}
System.out.println(sb);
}
static void printStar(int n, int x, int y) {
if( n == 1) {
cube[y][x] = "*";
return;
}
for(int j = 0 ; j < 3 ; j++) {
if( j != 1) {
for(int i = 0 ; i < 3 ; i++) {
printStar(n / 3, y + j * n / 3, x + i * n / 3);
}
}
else {
for(int i = 0 ; i < 3 ; i++) {
if(i != 1) {
printStar(n / 3, y + j * n / 3, x + i * n / 3);
}
else {
printSpace(n / 3, y + j * n / 3, x + i * n / 3);
}
}
}
}
}
static void printSpace(int n, int x, int y) {
for(int i = y ; i < y + n ; i++) {
for(int j = x ; j < x + n ; j++) {
cube[i][j] = " ";
}
}
}
}'알고리즘 공부 > 완전탐색' 카테고리의 다른 글
| 백준 1806 (부분합) (0) | 2021.04.25 |
|---|---|
| 백준 1759 (암호 만들기) - 조합알고리즘 (0) | 2021.04.14 |
| 프로그래머스 완전탐색 Level 2 (카펫) (0) | 2021.04.07 |
| 프로그래머스 완전탐색 Level 2 (소수 찾기) (0) | 2021.04.06 |
| 순열, 조합, 부분집합, 멱집합 정리 (0) | 2021.04.06 |