문제
병든 나이트가 N × M 크기 체스판의 가장 왼쪽아래 칸에 위치해 있다. 병든 나이트는 건강한 보통 체스의 나이트와 다르게 4가지로만 움직일 수 있다.
- 2칸 위로, 1칸 오른쪽
- 1칸 위로, 2칸 오른쪽
- 1칸 아래로, 2칸 오른쪽
- 2칸 아래로, 1칸 오른쪽
병든 나이트는 여행을 시작하려고 하고, 여행을 하면서 방문한 칸의 수를 최대로 하려고 한다. 병든 나이트의 이동 횟수가 4번보다 적지 않다면, 이동 방법을 모두 한 번씩 사용해야 한다. 이동 횟수가 4번보다 적은 경우(방문한 칸이 5개 미만)에는 이동 방법에 대한 제약이 없다.
체스판의 크기가 주어졌을 때, 병든 나이트가 여행에서 방문할 수 있는 칸의 최대 개수를 구해보자.
풀이
그림을 그려가며 풀어보니 총 4가지 경우가 있었다.
- N 이 1인경우
- N 이 2인경우
- N 이 3이상, M 이 7미만
- N 이 3이상, M 이 7이상
N 이 1인 경우는 최대 1로 할 수 있는 개수가 1개이다(시작점을 포함한다.)
N 이 2인 경우는 최대 4칸 까지 가능하다.(이유는 5이상의 칸을 여행하려면 1~4번까지를 모두 사용해야하지만 N 이 2면 1,4 번은 사용할 수 없다.)
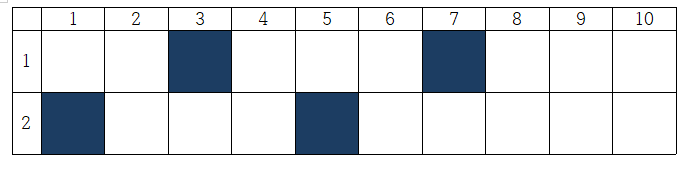
위 그림과 같이 보면된다.
M = 1 , 2 -> 1칸
M = 3 , 4 -> 2칸
M = 5 , 6 -> 3칸
M ≥ 7 -> 4칸
이 되므로 ( M + 1 ) / 2 가 4보다 크면 4 , 작으면 (M + 1) / 2 의 만큼 여행 할 수 있다.
N 이 3이상인 경우

최소 M 이 7 이상이여야 1~4번을 다 사용하여 5칸을 여행할 수 있다.
M이 7 이상인 경우는 M - 2 번을 여행 할 수 있고
M이 7 미만인 경우는 그림을 그려보면 M 번을 여행할 수 있다.( 단, 최대 4번까지)
이렇게 경우를 나누어 풀었다.
<코드>
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] num = br.readLine().split("\\s");
int n = Integer.parseInt(num[0]);
int m = Integer.parseInt(num[1]);
if(n == 1)
sb.append(1);
else if( n == 2)
sb.append( (m+1) / 2 > 4 ? 4 : (m+ 1) / 2);
else {
if(m < 7) {
sb.append( m > 4 ? 4 : m);
}else {
sb.append(m - 2);
}
}
System.out.println(sb);
}
}
'알고리즘 공부 > 탐욕알고리즘(Greedy)' 카테고리의 다른 글
| 백준 2873 (롤러코스터) (0) | 2021.01.21 |
|---|---|
| 백준 1931(회의실 배정) (0) | 2021.01.19 |
| 백준 10610 (30) / 배수판별법 (0) | 2021.01.17 |
| 백준 2875 ( 대회 or 인턴) (0) | 2021.01.17 |
| 백준 11047(동전 0) (0) | 2021.01.17 |